Find naked or hidden singles is the most basic strategy for solving a Sudoku. But how do you code a routine to do what a human does? First, let’s understand what a human does. See the learn sudoku page to see an example.
You need to find missing numbers in a row, column, and block (box). The intersection of the missing numbers in each group (row, column, and block) provides the possible solutions for a single cell. If there is only one solution possible, you have discovered a single.
def find_singles(grid: List[List[int]], box_size: int, row: int, col: int) -> Tuple[int, int, int] or None:
# Determine grid size (cells on a side)
grid_size = len(grid)
# Possible values based on grid size
candidates = set(range(1, grid_size + 1))
# Remove candidates found in row, column, and box
for i in range(grid_size):
candidates.discard(grid[row][i])
candidates.discard(grid[i][col])
box_row = box_size * (row // box_size)
box_col = box_size * (col // box_size)
for i in range(box_size):
for j in range(box_size):
candidates.discard(grid[box_row + i][box_col + j])
if len(candidates) == 1:
return row, col, candidates.pop()
else:
return NoneSeems simple enough. Most programmers will calculate potential candidates for each blank and update the potential candidates as cells are solved. This code repeatedly evaluates potential candidates instead of building on previous calculations.
The tradeoff is memory vs. speed. For small enough Sudokus it makes sense to save the information on potential candidates and update only what is necessary. You can even get clever and store potential candidates for each cell using bitwise functions.
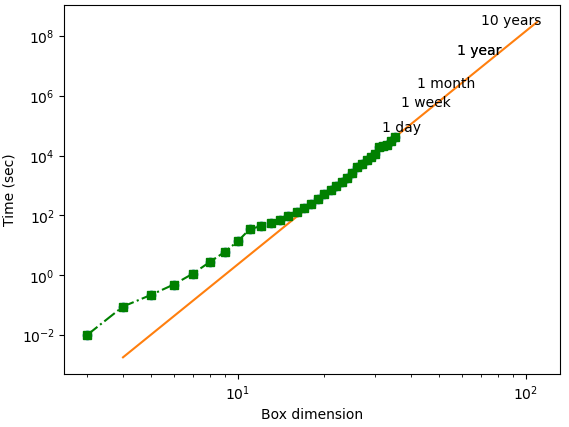
However, as Sudokus get larger, the memory required to save candidate information grows exponentially. For an n by n Sudoku memory requirements scale O(n^3). On a computer with 128GB RAM the matrix for candidates would limit you to a Sudoku with a box dimension of 100 or less.
For now, let’s assume that you do not want to save candidate information. So how can you optimize the code? One thought is to use the numpy libraries which are vector optimized.
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| |
Not what I expected. The results indicate quite an overhead of numpy relative to lists. In theory, numpy should perform better on large arrays. Are the arrays not large enough?
Since we are not saving results, the next best thing is to minimize expensive operations and reduce the number of times anything has to get calculated. Since many of the calculations are repetitive and can be reused, let’s save calculations where possible. The results below show that even though there is an overhead to numpy, eventually for large Sudokus numpy is faster that lists.
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
| |
The code for pre-calculating row, column, and box combinations but not storing candidates for every cell is provided below. Surprisingly, the code below runs 2-4 times faster than the base code once the Sudokus get really large (~30 or higher box dimensions).
def find_singlesNumpy(grid: np.ndarray, order: int, row: int, col: int, RowCandidates: List[List], ColCandidates: List[List], BoxCandidates: List[List]) -> tuple or None:
boxpos = order * (row // order) + (col // order)
candidates = reduce(np.intersect1d, (RowCandidates[row],ColCandidates[col],BoxCandidates[boxpos]))
if candidates.size == 1:
return row, col, candidates[0]
else:
return NoneWe’ll probably go back and try bit operations to see if we can speed up the solution of smaller Sudokus. It’s what everyone else does.
So how fast is the current solver? The current computer solve time uses 6 cores on computers with 128 GB RAM. The green dots indicate the puzzles we have solved so far. The target is to solve all puzzles 3600×3600 (box dimension 60) or smaller by July 2024.