Background
A few years ago I modified backtracking C code from Daniel Beer to generate and solve larger Sudoku puzzles (up to 1024×1024 grids). The elapsed time to solve larger and larger Sudoku puzzles climbed so quickly I started to look at alternative algorithms for solving and creating large Sudokus.
The current solvers use single core SAT solvers (go based) or dancing link python code. The codes seem to work well as long as there aren’t too many blanks – particularly when the puzzles start to get larger.
At the current time the dancing link code runs into recursion limits – or so it seems – around Sudokus with a box dimension of 10 == 100×100 grids. Turns out Windows implementations of python have a fixed stack size. Changes require spawning a new thread with a higher stack size limit. The nice feature of using Knuth’s dancing links is that you can identify puzzles with multiple solutions. Now we can solve grids up to 225×225 in 1028 seconds (box dimension of 15) without crashing my computer. Note how quickly the computation times increase with grid size. Also, these times (dancing links) are at least 1-2 orders of magnitude larger than the hidden/naked singles strategy solver for our “easy” Sudokus.
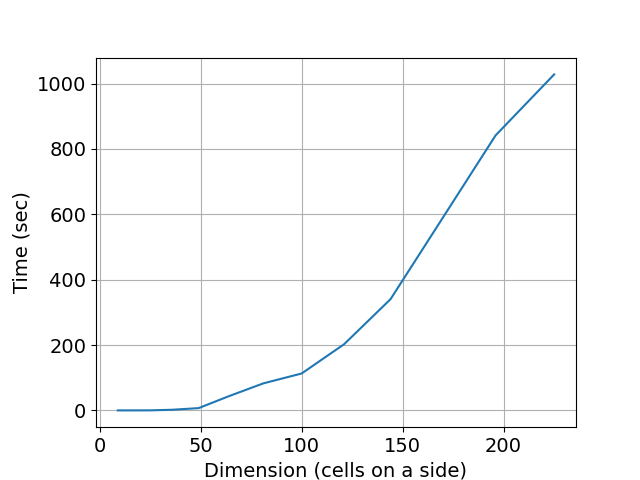
The SAT solver is good for puzzles up to a box dimension of 20 or so. If the blank percentage is closer to 25-33% the same SAT solver can solve 961×961 grids. The speed is great but it doesn’t make for a generalized solver – at least for really large dimensions.
SAT Challenges
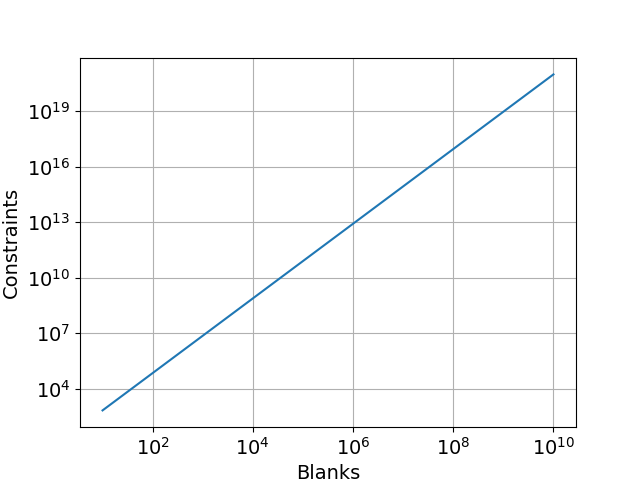
One of the reasons a SAT solver runs out of memory is the number of constraints necessary to describe a Sudoku puzzle. Note that box dimensions of 235 or greater (grid dimension of 55225×55225) lead to a ridiculous number of constraints. So many constraints that can overwhelm even an unsigned 64 bit integer. Most computers would likely run out of memory long before you had to handle that many constraints.
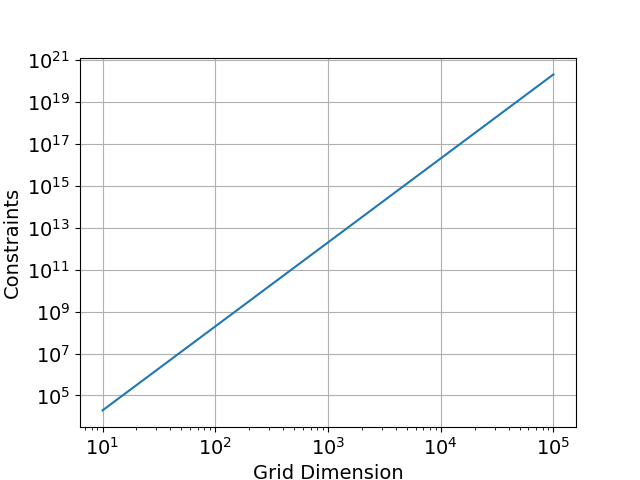
Let’s look at the exponential growth of constraints. The number of blanks in a puzzle drive the number of constraints. The largest Sudokus in print vary from the 36×36 grid variety (box dimension = 6) with ~700 blanks or so to 81×81 grids.
Our current efforts focus on parallel solvers (GPU or multicore machines). If you have any suggestions we’re open to ideas.
So why should anyone care about solving ridiculously large Sudokus? Dealing with large dimensional solution spaces is not limited to large Sudoku problems. More practical engineering, scientific, and even security challenges need to work in large solution spaces. It’s game time!